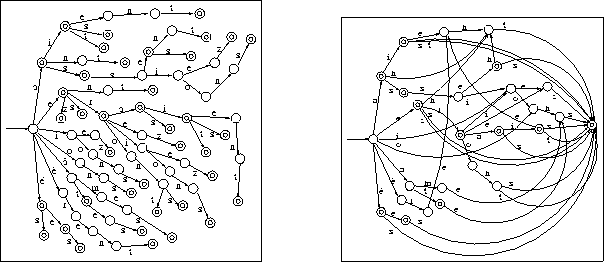
Figure 4.3: The unique minimal DAFSA whose language is the French regular
endings of verbs of the first group
Figure 4.2: A trie whose language is the French regular endings of verbs
of the first group
A trie is a deterministic acyclic finite-state automaton (DAFSA) whose transition graph is a trie with the initial state as the root and all leaves being final. Let us imagine an FSA in a form of a trie (figure 4.2, for example). We can see that many subtrees are isomorphic. The minimal DAFSA (fig. 4.3) is the one where, for all isomorphic trees, only one copy is kept, (pointers to all pairwise isomorphic subtrees are replaced by pointers to their unique copy).
Traditionally, to obtain a minimal DAFSA one would first create a DAFSA for the language (not necessarily minimal), and then minimize it using any of a number of well known algorithms (see [Wat93b] and [Wat95]). Usually the first stage is done by building a trie. Algorithms that minimize DAFSA can be fairly effective in their use of memory, but the size of the original automaton can be huge, although some effort towards decreasing memory requirements for it has been reported ([Rev91]). We present a way to reduce these intermediate memory requirements and total construction time by constructing the minimal automaton incrementally (word by word, maintaining an invariant of minimality) as soon as new data arrives, thus avoiding ever having a trie in memory.
The central part of all FSA minimization
algorithms is a classification of states
([Wat93b], [Wat95]). The states of a
DAFSA are partitioned into classes of abstractions whose
representatives are the states of the minimal DAFSA .
Assuming the original dictionary does not have any useless states
(
is true), then we can see (by the definition of
minimality we use) that each state in the minimal DAFSA must have a
unique right language .
Since this is a necessary and sufficient condition for minimality, we
can use equality of right
languages as our
equivalence relation for our classes ([Wat93b],
[Wat95]). Using the given definition of right
languages, it is easily shown that equality of right languages is an
equivalence relation (reflexive, symmetric and transitive). We will
denote two states, p and q, belonging to the same equivalence
class by 
.
Let us walk through a minimization of the trie in figure 4.2 using the algorithm given in [HU79]. Initially, only pairs of states where one is final, and the other is not, can be recognized and marked as belonging to different classes. Pairs of states that have a different number of out transitions or the same number with different labels, can be marked as different. Then pairs of states that have transitions labeled with the same symbols, but leading to states that have already been considered and are marked as different, can immediately be marked as different.